The STA-ImageAnalysisToolkit namespace. More...

Classes
class	_stafield
	represents spherical tensor fields More...

class	CtimeStopper

class	Fourier

class	Gauss

class	GaussBessel

class	GaussLaguerre

class	Kernel

class	SH

class	sta_fspecial_func

class	STAError
	the STA error class More...

class	stafield
	represents spherical tensor fields (CPU version) More...

class	stafieldGPU
	represents spherical tensor fields (GPU version) More...

Enumerations
enum	STA_RESULT
	function return value

enum	STA_FIELD_STORAGE { , STA_FIELD_STORAGE_C =2, STA_FIELD_STORAGE_R =4, STA_FIELD_STORAGE_RF =8 }
	tensor field data storage More...

enum	STA_FIELD_TYPE { , STA_OFIELD_SINGLE =128, STA_OFIELD_FULL =256, STA_OFIELD_EVEN =512, STA_OFIELD_ODD =1024 }
	tensor field data interpretations according to certain symmetries More...

Functions
template<typename T >
STA_RESULT	sta_product (const std::complex< T > stIn1, const std::complex< T > stIn2, std::complex< T > *stOut, const std::size_t shape[], int J1, int J2, int J, std::complex< T > alpha=T(1), bool normalize=false, STA_FIELD_STORAGE field_storage=STA_FIELD_STORAGE_C, int stride_in1=-1, int stride_in2=-1, int stride_out=-1, bool clear_field=false)
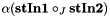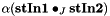	spherical tensor product: $\alpha(\mathbf{stIn1} \circ_{J} \mathbf{stIn2})$ and $\alpha(\mathbf{stIn1} \bullet_{J} \mathbf{stIn2})$ , respectively More...

template<typename T , typename S >
STA_RESULT	sta_mult (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int ncomponents, S alpha=S(1), bool conjugate=false, int stride_in=-1, int stride_out=-1, bool clear_field=false)
	computes $\alpha(\mathbf{stIn})$ More...

template<typename T >
STA_RESULT	sta_norm (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int J, STA_FIELD_STORAGE field_storage=STA_FIELD_STORAGE_C, int stride_in=-1, int stride_out=-1, bool clear_field=false)
	returns lengths of vectors component by compnent More...

template<typename T >
STA_RESULT	sta_derivatives (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int J, int Jupdown, bool conjugate=false, std::complex< T > alpha=(T) 1.0, STA_FIELD_STORAGE field_storage=STA_FIELD_STORAGE_C, const T v_size[]=NULL, int stride_in=-1, int stride_out=-1, bool clear_field=false, int accuracy=0)
	spherical tensor derivative: 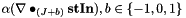$\alpha( {\nabla} \bullet_{(J+b)} \mathbf{stIn}) , b \in \{-1,0,1\}$ More...

template<typename T >
STA_RESULT	sta_derivatives2 (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int J, int Jupdown, bool conjugate=false, std::complex< T > alpha=(T) 1.0, STA_FIELD_STORAGE field_storage=STA_FIELD_STORAGE_C, const T v_size[]=NULL, int stride_in=-1, int stride_out=-1, bool clear_field=false)
	spherical tensor double-derivative: 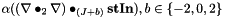$\alpha(({\nabla} \bullet_{2} {\nabla}) \bullet_{(J+b)} \mathbf{stIn}), b \in \{-2,0,2\}$ More...

template<typename T >
STA_RESULT	sta_laplace (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int components=1, int type=1, std::complex< T > alpha=1, STA_FIELD_STORAGE field_storage=STA_FIELD_STORAGE_C, const T v_size[]=NULL, int stride_in=-1, int stride_out=-1, bool clear_field=false)
	Laplacian: 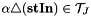$\alpha\triangle(\mathbf{stIn}) \in \mathcal T_{J}$ . More...

template<typename T , typename S >
STA_RESULT	sta_fft (const std::complex< T > stIn, std::complex< T > stOut, const std::size_t shape[], int components, bool forward, bool conjugate=false, S alpha=(S) 1, int flag=0)
	tensor fft component by component More...

Detailed Description

The STA-ImageAnalysisToolkit namespace.

Enumeration Type Documentation

enum hanalysis::STA_FIELD_STORAGE

tensor field data storage

Enumerator
STA_FIELD_STORAGE_C	no symmetry. The tensor-data should be arranged as follows: $(\mathbf a^\ell_{-\ell},\mathbf a^\ell_{-(\ell-1)} \cdots,\mathbf a^\ell_{-1},\mathbf a^\ell_{0},\mathbf a^\ell_{1},\cdots,\mathbf a^\ell_{(\ell-1)},\mathbf a^\ell_{\ell})$
STA_FIELD_STORAGE_R	we assume the following symmetry: $\mathbf a^\ell_m(\mathbf x)=(-1)^m \overline{\mathbf a^\ell_{-m}(\mathbf x) }$ . Tensor-data should be arranged as follows: $(\mathbf a^\ell_{-\ell},\mathbf a^\ell_{-(\ell-1)} \cdots,\mathbf a^\ell_{-1},\mathbf a^\ell_{0})$
STA_FIELD_STORAGE_RF	we assume the following symmetry: $\mathbf a^\ell_m(\mathbf k)=(-1)^m \overline{\mathbf a^\ell_{-m}(-\mathbf k) }$ . Tensor-data should be arranged as follows: $(\mathbf a^\ell_{-\ell},\mathbf a^\ell_{-(\ell-1)} \cdots,\mathbf a^\ell_{-1},\mathbf a^\ell_{0})$

enum hanalysis::STA_FIELD_TYPE

tensor field data interpretations according to certain symmetries

Enumerator
STA_OFIELD_SINGLE	tensor field has one single component of rank : $\ell$
STA_OFIELD_FULL	tensor field has all components of ranks : $[ 0, \cdots, \ell ]$
STA_OFIELD_EVEN	tensor field has all components of even ranks : $[0, \cdots,\ell_m,\cdots, \ell] ,~ (\ell_m \% 2==0)$
STA_OFIELD_ODD	tensor field has all components of odd ranks : $[1, \cdots,\ell_m,\cdots, \ell] ,~ (\ell_m \% 2==1)$

Function Documentation

template<typename T >

STA_RESULT hanalysis::sta_derivatives	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	J,
		int	Jupdown,
		bool	conjugate = `false`,
		std::complex< T >	alpha = `( T ) 1.0`,
		STA_FIELD_STORAGE	field_storage = `STA_FIELD_STORAGE_C`,
		const T	v_size[] = `NULL`,
		int	stride_in = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`,
		int	accuracy = `0`
	)

spherical tensor derivative: 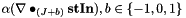$\alpha( {\nabla} \bullet_{(J+b)} \mathbf{stIn}) , b \in \{-1,0,1\}$

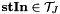
computes the spherical tensor derivative of $\mathbf{stIn} \in \mathcal T_{J}$

Parameters

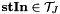stIn	$\mathbf{stIn} \in \mathcal T_{J}$
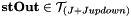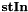stOut	$\mathbf{stOut} \in \mathcal T_{(J+Jupdown)}$ , the spherical tensor derivative of $\mathbf{stIn}$
shape
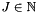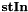J	$J \in \mathbb N$ tensor rank of the input field $\mathbf{stIn}$
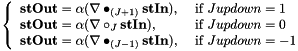Jupdown	$\left\{ \begin{array}{ll} \mathbf{stOut}=\alpha({\nabla} \bullet_{(J+1)} \mathbf{stIn}), & \mbox{ if } Jupdown=1\\ \mathbf{stOut}=\alpha({\nabla} \circ_{J} \mathbf{stIn}), & \mbox{ if } Jupdown=0\\ \mathbf{stOut}=\alpha({\nabla} \bullet_{(J-1)} \mathbf{stIn}), & \mbox{ if } Jupdown=-1 \end{array} \right.$
conjugate	if conjugate=true the conjugate operator $\overline{{\nabla}}$ is used
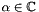alpha	$\alpha \in \mathbb C$ additional weighting factor

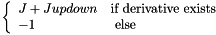
Returns: $\left\{ \begin{array}{ll} J+Jupdown & \mbox{if derivative exists}\\ -1 & \mbox{ else } \end{array} \right.$

Warning: ensure that stIn, stOut and shape exist and have been allocated properly!; if not STA_FIELD_STORAGE_C then alpha must be real valued

template<typename T >

STA_RESULT hanalysis::sta_derivatives2	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	J,
		int	Jupdown,
		bool	conjugate = `false`,
		std::complex< T >	alpha = `( T ) 1.0`,
		STA_FIELD_STORAGE	field_storage = `STA_FIELD_STORAGE_C`,
		const T	v_size[] = `NULL`,
		int	stride_in = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`
	)

spherical tensor double-derivative: 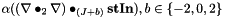$\alpha(({\nabla} \bullet_{2} {\nabla}) \bullet_{(J+b)} \mathbf{stIn}), b \in \{-2,0,2\}$

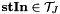
computes the spherical tensor double-derivative of $\mathbf{stIn} \in \mathcal T_{J}$

Parameters

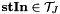stIn	$\mathbf{stIn} \in \mathcal T_{J}$
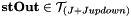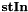stOut	$\mathbf{stOut} \in \mathcal T_{(J+Jupdown)}$ , the spherical tensor double-derivative of $\mathbf{stIn}$
shape
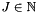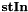J	$J \in \mathbb N$ tensor rank of the input field $\mathbf{stIn}$
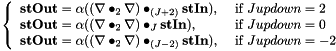Jupdown	$\left\{ \begin{array}{ll} \mathbf{stOut}=\alpha(({\nabla} \bullet_{2} {\nabla}) \bullet_{(J+2)} \mathbf{stIn}), & \mbox{ if } Jupdown=2\\ \mathbf{stOut}=\alpha(({\nabla} \bullet_{2} {\nabla}) \bullet_{J} \mathbf{stIn}), & \mbox{ if } Jupdown=0\\ \mathbf{stOut}=\alpha(({\nabla} \bullet_{2} {\nabla}) \bullet_{(J-2)} \mathbf{stIn}), & \mbox{ if } Jupdown=-2 \end{array} \right.$
conjugate	if conjugate=true the conjugate operator $\overline{{\nabla}}$ is used
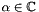alpha	$\alpha \in \mathbb C$ additional weighting factor

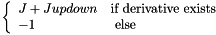
Returns: $\left\{ \begin{array}{ll} J+Jupdown & \mbox{if derivative exists}\\ -1 & \mbox{ else } \end{array} \right.$

Warning: ensure that stIn, stOut and shape exist and have been allocated properly!; if not STA_FIELD_STORAGE_C then alpha must be real valued

template<typename T , typename S >

STA_RESULT hanalysis::sta_fft	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	components,
		bool	forward,
		bool	conjugate = `false`,
		S	alpha = `( S ) 1`,
		int	flag = `0`
	)

tensor fft component by component

transforms a spherical tensor field 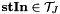$\mathbf{stIn} \in \mathcal T_{J}$ into Fourier domain (and back)

Parameters

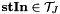stIn	$\mathbf{stIn} \in \mathcal T_{J}$
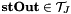stOut	$\mathbf{stOut} \in \mathcal T_{J}$
shape
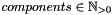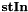components	$components \in \mathbb N_{>0}$ , number of tensor components of the input field $\mathbf{stIn}$
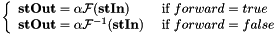forward	$\left\{ \begin{array}{ll} \mathbf{stOut}=\alpha\mathcal F (\mathbf{stIn}) & \mbox{ if } forward=true \\ \mathbf{stOut}=\alpha\mathcal F^{-1} (\mathbf{stIn}) & \mbox{ if } forward=false \end{array} \right.$
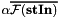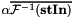conjugate	if true it computes $\alpha\overline{\mathcal F (\mathbf{stIn})}$ and $\alpha\overline{\mathcal F^{-1} (\mathbf{stIn})}$ , respectively
alpha	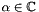$\alpha \in \mathbb C$ additional weighting factor

Warning: ensure that stIn, stOut and shape exist and have been allocated properly!
Consider that $\frac{\mathcal F^{-1}(\mathcal F (\mathbf{stIn}))}{shape[0] \cdot shape[1] \cdot shape[2]}=\mathbf{stIn}$ !!

template<typename T >

STA_RESULT hanalysis::sta_laplace	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	components = `1`,
		int	type = `1`,
		std::complex< T >	alpha = `1`,
		STA_FIELD_STORAGE	field_storage = `STA_FIELD_STORAGE_C`,
		const T	v_size[] = `NULL`,
		int	stride_in = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`
	)

Laplacian: 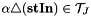$\alpha\triangle(\mathbf{stIn}) \in \mathcal T_{J}$ .

computes the Laplacian of 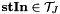$\mathbf{stIn} \in \mathcal T_{J}$ component by component

Parameters

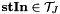stIn	$\mathbf{stIn} \in \mathcal T_{J}$
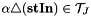stOut	$\alpha\triangle(\mathbf{stIn}) \in \mathcal T_{J}$
shape
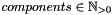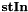components	$components \in \mathbb N_{>0}$ number of tensor components of the input field $\mathbf{stIn}$
type	if type=1 the standard 6 neighbors operator is used, if type=0 a 18 neighbors operator is used
alpha	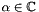$\alpha \in \mathbb C$ additional weighting factor

Warning: ensure that stIn, stOut and shape exist and have been allocated properly!

template<typename T , typename S >

STA_RESULT hanalysis::sta_mult	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	ncomponents,
		S	alpha = `S ( 1 )`,
		bool	conjugate = `false`,
		int	stride_in = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`
	)

computes $\alpha(\mathbf{stIn})$

multiplication with a scalar: $\alpha(\mathbf{stIn})$

Parameters

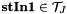stIn	$\mathbf{stIn1} \in \mathcal T_{J}$
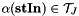stOut	$\alpha(\mathbf{stIn}) \in \mathcal T_{J}$
shape
ncomponents	number of tensor components
alpha	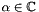$\alpha \in \mathbb C$ weighting factor
conjugate	returns 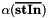$\alpha(\overline{\mathbf{stIn}})$ if true

Warning: ensure that stIn, stOut and shape exist and have been allocated properly!

template<typename T >

STA_RESULT hanalysis::sta_norm	(	const std::complex< T > *	stIn,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	J,
		STA_FIELD_STORAGE	field_storage = `STA_FIELD_STORAGE_C`,
		int	stride_in = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`
	)

returns lengths of vectors component by compnent

Parameters

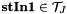stIn	$\mathbf{stIn1} \in \mathcal T_{J}$
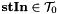stOut	$\mathbf{stIn} \in \mathcal T_{0}$
shape
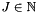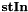J	$J \in \mathbb N$ tensor rank of the input field $\mathbf{stIn}$

template<typename T >

STA_RESULT hanalysis::sta_product	(	const std::complex< T > *	stIn1,
		const std::complex< T > *	stIn2,
		std::complex< T > *	stOut,
		const std::size_t	shape[],
		int	J1,
		int	J2,
		int	J,
		std::complex< T >	alpha = `T( 1 )`,
		bool	normalize = `false`,
		STA_FIELD_STORAGE	field_storage = `STA_FIELD_STORAGE_C`,
		int	stride_in1 = `-1`,
		int	stride_in2 = `-1`,
		int	stride_out = `-1`,
		bool	clear_field = `false`
	)

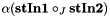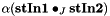spherical tensor product: $\alpha(\mathbf{stIn1} \circ_{J} \mathbf{stIn2})$ and $\alpha(\mathbf{stIn1} \bullet_{J} \mathbf{stIn2})$ , respectively

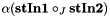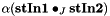computes the spherical tensor product $\alpha(\mathbf{stIn1} \circ_{J} \mathbf{stIn2})$ and $\alpha(\mathbf{stIn1} \bullet_{J} \mathbf{stIn2})$ , respectively

Parameters

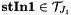stIn1	$\mathbf{stIn1} \in \mathcal T_{J_1}$
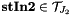stIn2	$\mathbf{stIn2} \in \mathcal T_{J_2}$
stOut	$\alpha(\mathbf{stIn1} \bullet_{J} \mathbf{stIn2}) \in \mathcal T_{J}$ if normalized, $\alpha(\mathbf{stIn1} \circ_{J} \mathbf{stIn2}) \in \mathcal T_{J}$ else
shape
J1	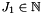$J_1 \in \mathbb N$ tensor rank of the first field
J2	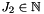$J_2 \in \mathbb N$ tensor rank of the second field
J	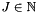$J \in \mathbb N$ tensor rank of the resulting field
alpha	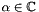$\alpha \in \mathbb C$ additional weighting factor
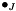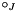normalize	normalized tensor products?: true= $\bullet_{J}$ , false= $\circ_{J}$

Returns: $\left\{ \begin{array}{ll} 0 & \mbox{if tensor product exists}\\ -1 & \mbox{ else } \end{array} \right.$

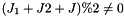Warning: ensure that stIn1, stIn2, stOut and shape exist and have been allocated properly!; If field_storage=STA_FIELD_STORAGE_R and $(J_1+J2+J)\%2 \neq 0$ the function returns
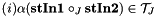$(\mathit{i})\alpha(\mathbf{stIn1} \circ_{J} \mathbf{stIn2}) \in \mathcal T_{J}$ . This ensures that STA_FIELD_STORAGE_R holds for 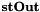$\mathbf{stOut}$ , too.
The same is true for field_storage=STA_FIELD_STORAGE_RF; if not STA_FIELD_STORAGE_C then alpha must be real valued

Classes

Enumerations

Functions

Detailed Description

Enumeration Type Documentation

Function Documentation