|
| stafield & | operator= (const stafield &f) |
| |
| stafield & | operator+= (const stafield &a) |
| |
| stafield & | operator-= (const stafield &a) |
| |
| stafield & | operator*= (std::complex< T > alpha) |
| |
| stafield & | operator/= (std::complex< T > alpha) |
| |
| const stafield | operator+ (const stafield &a) const |
| |
| const stafield | operator- (const stafield &a) const |
| |
| const stafield | operator* (std::complex< T > alpha) const |
| |
| const stafield | operator/ (std::complex< T > alpha) const |
| |
| stafield | operator[] (int l) const |
| |
| | stafield (const std::size_t shape[], int L, hanalysis::STA_FIELD_STORAGE field_storage=hanalysis::STA_FIELD_STORAGE_R, hanalysis::STA_FIELD_TYPE field_type=hanalysis::STA_OFIELD_SINGLE, const T element_size[]=NULL) |
| |
| | stafield (std::string kernelname, const std::size_t shape[], std::vector< T > param_v, bool centered=false, int L=0, hanalysis::STA_FIELD_STORAGE field_storage=hanalysis::STA_FIELD_STORAGE_R, const T element_size[]=NULL) |
| |
| | stafield (const std::size_t shape[], int L, hanalysis::STA_FIELD_STORAGE field_storage, hanalysis::STA_FIELD_TYPE field_type, std::complex< T > *data, std::size_t stride=0, const T element_size[]=NULL) |
| |
| bool | createMemCopy () |
| |
| std::complex< T > * | getData () |
| |
| const std::complex< T > * | getDataConst () const |
| |
| stafield | get (int l) const |
| |
|
stafield | fft (bool forward, bool conjugate=false, std::complex< T > alpha=T(1), int flag=0) const |
| | see FFT
|
| |
|
stafield | convolve (stafield &b, int J=0, int flag=0) |
| | see FFT
|
| |
|
stafield | mult (std::complex< T > alpha=T(1), bool conjugate=false) const |
| | see Mult
|
| |
|
stafield | norm () const |
| | see Norm
|
| |
|
stafield | deriv (int J, bool conjugate=false, std::complex< T > alpha=T(1), int accuracy=0) const |
| | see Deriv
|
| |
|
stafield | deriv2 (int J, bool conjugate=false, std::complex< T > alpha=T(1), int accuracy=0) const |
| | see Deriv2
|
| |
|
stafield | lap (std::complex< T > alpha=T(1), int type=1) const |
| | see Lap
|
| |
|
stafield | prod (const stafield &b, int J, bool normalize=false, std::complex< T > alpha=T(1)) const |
| | see Prod
|
| |
|
stafield | exp (std::complex< T > value=T(1)) const |
| | exp, component by component
|
| |
|
stafield | sqrt () const |
| | sqrt, component by component
|
| |
|
stafield | pow (T v=T(1)) const |
| | pow, component by component
|
| |
|
stafield | invert (T v=std::numeric_limits< T >::epsilon()) const |
| | invert, component by component
|
| |
| bool | operator== (const _stafield &field) const |
| |
| bool | operator!= (const _stafield &field) const |
| |
| const std::size_t * | getShape () const |
| |
| bool | ownMemory () const |
| |
| int | getRank () const |
| |
|
| static void | FFT (const stafield &stIn, stafield &stOut, bool forward, bool conjugate=false, std::complex< T > alpha=T(1), int flag=0) |
| | tensor fft component by component More...
|
| |
| static void | Mult (const stafield &stIn, stafield &stOut, std::complex< T > alpha=T(1), bool conjugate=false, bool clear_result=false) |
| | computes  More... More...
|
| |
| static void | Norm (const stafield &stIn, stafield &stOut, bool clear_result=false) |
| | returns lengths of vectors component by compnent
More...
|
| |
| static void | Deriv (const stafield &stIn, stafield &stOut, int Jupdown, bool conjugate=false, std::complex< T > alpha=T(1), bool clear_result=false, int accuracy=0) |
| | spherical tensor derivative: 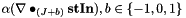 More... More...
|
| |
| static void | Deriv2 (const stafield &stIn, stafield &stOut, int Jupdown, bool conjugate=false, std::complex< T > alpha=T(1), bool clear_result=false) |
| | spherical tensor double-derivative: 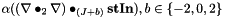 More... More...
|
| |
| static void | Lap (const stafield &stIn, stafield &stOut, std::complex< T > alpha=T(1), bool clear_result=false, int type=1) |
| | Laplacian: 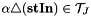 . More... . More...
|
| |
| static void | Prod (const stafield &stIn1, const stafield &stIn2, stafield &stOut, int J, bool normalize=false, std::complex< T > alpha=T(1), bool clear_result=false) |
| | spherical tensor product: 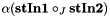 and and 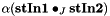 , respectively , respectively
More...
|
| |
template<typename T>
class hanalysis::stafield< T >
represents spherical tensor fields (CPU version)
 Public Member Functions inherited from hanalysis::_stafield< T >
Public Member Functions inherited from hanalysis::_stafield< T > More...
More...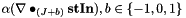 More...
More...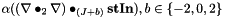 More...
More...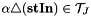 . More...
. More...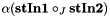 and
and 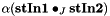 , respectively
, respectively  Protected Attributes inherited from hanalysis::_stafield< T >
Protected Attributes inherited from hanalysis::_stafield< T >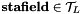
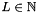
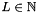 , the tensor rank
, the tensor rank 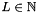
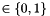
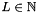 , the tensor rank
, the tensor rank 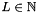
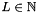 , the tensor rank
, the tensor rank 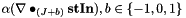
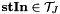
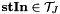
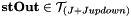 , the spherical tensor derivative of
, the spherical tensor derivative of 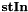
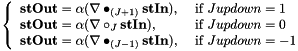
 is used
is used 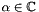 additional weighting factor
additional weighting factor 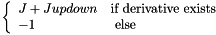
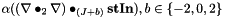
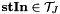
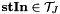
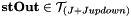 , the spherical tensor double-derivative of
, the spherical tensor double-derivative of 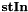
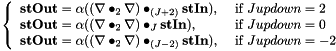
 is used
is used 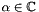 additional weighting factor
additional weighting factor 
 into Fourier domain (and back)
into Fourier domain (and back) 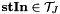
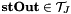
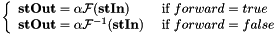
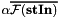 and
and 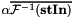 , respectively
, respectively 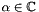 additional weighting factor
additional weighting factor ![$ \frac{\mathcal F^{-1}(\mathcal F (\mathbf{stIn}))}{shape[0] \cdot shape[1] \cdot shape[2]}=\mathbf{stIn} $](form_20.png) !!
!! 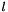 with the
with the 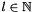 of an orientation tensor field
of an orientation tensor field 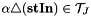 .
. 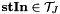 component by component
component by component 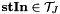
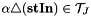
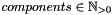 number of tensor components of the input field
number of tensor components of the input field 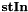
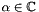 additional weighting factor
additional weighting factor 

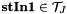
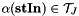
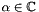 weighting factor
weighting factor 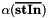 if true
if true 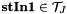
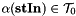

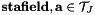
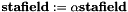
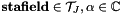

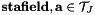
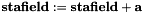
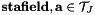

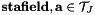
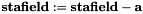
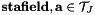

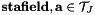
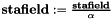
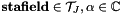
 . Allocates new memory only when necessary
. Allocates new memory only when necessary 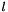 with the
with the 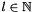 of an orientation tensor field
of an orientation tensor field 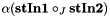 and
and 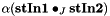 , respectively
, respectively 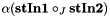 and
and 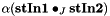 , respectively
, respectively 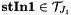
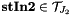
 if normalized,
if normalized,  else
else 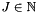 tensor rank of the resulting field
tensor rank of the resulting field 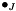 , false=
, false= 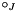
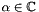 additional weighting factor
additional weighting factor 
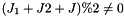 the function returns
the function returns 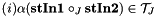 . This ensures that STA_FIELD_STORAGE_R holds for
. This ensures that STA_FIELD_STORAGE_R holds for 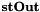 , too.
, too.  1.8.9.1
1.8.9.1