わたしがMATLAB上で書いて使用している 簡単なソフトウェアのうち、比較的応用範囲が広そうなものを公開します。
21 Aug. 2002 : とりあえず公開
k 平均法によるクラスタリングを行います。
使用法
>> [mu, S, N] = kmeans( X, m )
ただし、 X は入力横ベクトルを 縦に並べて作った行列。 m はクラスタ数。 出力 mu は クラスタ中心の横ベクトルを 縦にクラスタ数ぶん並べて作った行列。 S は各クラスタ内データのスカラー分散。 N は各クラスタに属するデータ個数。
整数値を持つことが分かっている行列データをアスキーで出力します。 普通のセーブでは、浮動小数点で書き出されてしまってうざいでしょ？
使用法
>> saveInt('filename.dat',A)
デターミナントの対数を求めます。 単にdet(x)でデターミナントを計算してからその対数をとるのでは、 とくに行列がでかいときに値が浮動小数点でも表現できなくなったりして困ります。 行列を対角化してから、対角成分の対数の和をとることで安定した計算ができます。
digamma 関数は gamma 関数の 対数の微分です。 MATLABが持つ gammaln 関数を数値微分することによってこれを計算しています。
図式表示(schematic plot)とは下図のようなものである。
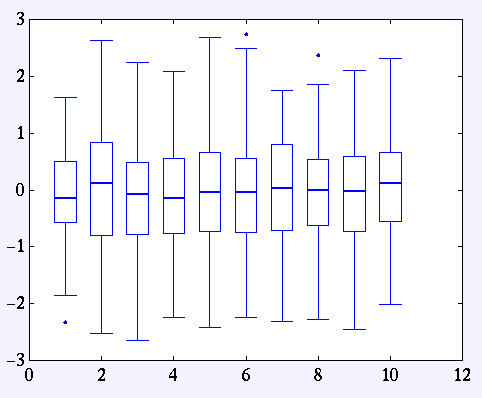
各ろうそく状の図は以下のような意味をもつ。
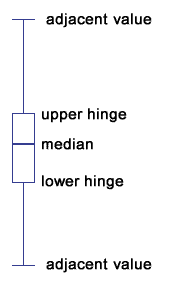
上側ヒンジ(upper hinge)とは、中央値よりも大きな値のデータのみ取り出したとき、
さらにその中央値のことである。
下側ヒンジ(lower hinge)とは同様に中央値よりも小さなデータの中央値である。
上下ヒンジ間範囲の大きさを 1 ヒンジ散布度という。
2つの隣接値(adjacent value)とは、
上側が 上側ヒンジ + 1.5 ヒンジ散布度 よりも内側にある最大のデータ値
で定義され、
下側が 下側ヒンジ - 1.5 ヒンジ散布度 よりも内側にある最小のデータ値
で定義される。
隣接値よりも外側の値を外側値(outside value)と呼び、省略せずに点で表示する。
使用法
>> label = [ 1 2 2 2 2 2 2 2 1 1 1 1 2 1 ];
>> y = [ 0.96 0.30 0.77 0.89 0.25 0.14 0.34 ...
0.73 0.03 0.54 0.55 0.66 0.58 0.68 ]
>> schematicplot( label, y )
データベクトル y の各成分について、整数値ラベル label がついているとき、 ラベルごとのデータ値の分布を「図式表示」する。