Statistical Learning
Data and learning
Our research on statistical learning intends to derive various knowledge from statistical characters in the observed data. We human being estimate the future development of the objects based on such a knowledge, and we make better decision. The reinforcement learning method is one of the applications of statistical learning, which looking for an optimum action policy based on a reward.
We investigate various ways of knowledge expression by means of probabilistic models, such as:
-
Gaussian mixture model
Data are generated from a mixture of multiple clusters each of which is normally distributed. -
NGnet (normalized Gaussian network)
The input space is softly divided by normal distribution, and in each part, the input-output relationship is approximated by linear model. -
Mixture of principal component analyzers (MPCA)
Almost same with Gaussian mixture model, except that, each of cluster is expressed by principal axes. -
Gaussian process model
The function, which determine input/output relation, is derived from a Gaussian process.
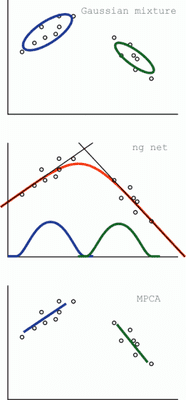
Simultaneous analysis of clustering analysis and principal component analysis
Gaussian mixture model assumes that the data distribution is generated from a mixture of clusters each of which is Gaussian. And it is often used for unsupervised clustering analysis and supervised classification analysis. Normal distribution does not have rigid edge and makes fuzzy devision between the clusters. However, it has many problems when applying it to high-dimensional data.
- Using isotropic normal distribution cluster, the model becomes too simple to fit the data.
- Using normal distribution with full covariance matrix, the model becomes too complex. It causes:
- computational explosion
- over fitting to the noise contained data
- divergence of computation from singular covariance matrix
Mixture of principal component analyzers overcome such problems by means of a new way of expression of covariance matrix. The covariance matrix is expressed by an appropriate number of principal axes and the degree of freedom becomes appropriately smaller. We apply a Bayesian model selection method, and realized cluster number estimation and dimensionality estimation.
See also,
- Oba, S., Sato, M. & Ishii, S. On-line Learning Methods for Gaussian Processes. IEICE Transactions on Information and Systems, E86-D(3), pp. 650-654 (2003).
- S. Oba, M. Sato and S. Ishii: Variational Bayes method for mixture of principal component analyzers. Systems and Computers in Japan, (to appear)
- Yoshimoto, J., Ishii, S. & Sato, M. (2002). Hierarchical model selection for NGnet based on variational Bayes inference. [ps] [pdf] in Artificial Neural Networks - ICANN 2002, Lecture Notes in Computer Science 2415, pp.661-666, Springer Verlag.