Reinforcement Learning (RL)
RL is a machine learning framework to acquire an optimal action policy based on actual experiences and rewards. Although a learning agent in supervised learning domain can directly know some inputs and their desired outputs, the RL agent can only observe a current input (state) and its abstract desirability (reward). Moreover, the subsequent states depends on the current action. In such a environment, the RL agent tries to make decision so as to maximize total rewards.
Let me consider a situation where we play a game, for example, chess, checker and so on. We probably lose the game in the initial stage because we little know how to play. However, as we repeat the game more times, we will obtain a better strategy and finally become its expert. RL methods provide a mathematical approach to reveal the mechanism of such a intelligence.
In our laboratory, we develop an RL method for automatic control problems in continuous state and action spaces and apply it to the following tasks. We expect that these methods will be useful for modeling the mechanism of the human learning from motion sequences.
1. Inverted Pendulum
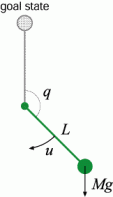
The task is to swing up and stabilize a single pendulum at the upright position. Figure 1 shows a model of this task. If the agent know physical properties (i.e. the mass, the inertia moment, the friction and so on) of the pendulum and the exerted torque is unlimited, this control task is very easy.
However, we assume three conditions:
- The agent (controller) do not know physical properties of controlled object in advance.
- The agent can observe the state variables (angle and angular velocity) of the pendulum and exert a torque at every step.
- The exerted torque is not large enough to bring the pendulum up without several swinging.
The first and second conditions is natural in the real world. The last condition means that we have to build a nonlinear controller. The RL method is very useful for determining a good control policy under such a environment.
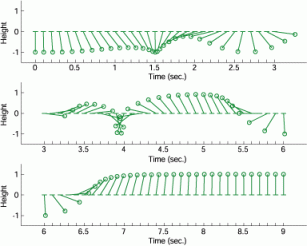
Our proposed RL method can obtain a fairly good policy with a few learning states. Figure 2 shows that a typical control process after 17 learning episodes, where a learning episodes is defined as 7 seconds. If you are interested in this topic, we recommend you to see [1].
2. Acrobot
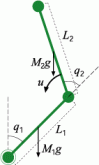
Acrobot is a two-link underactuated robot depicted in figure 4. It is analogous to a gymnast swinging on a high bar. The second joint (corresponding to the gymnast's waist) exerts torque, while the first joint (corresponding to the gymnast's hands on the bar) does not. The goal of this task is to balance the acrobot at the vicinity of the upright position. This is a very more difficult RL task than the inverted pendulum task because the system is terribly nonlinear and unstable.
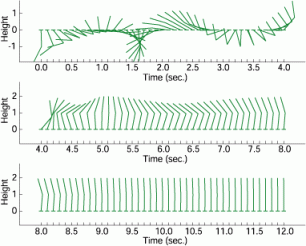
However, our method realizes an efficient learning. If the initial state is set at the vicinity of the upright position, our method is able to balance the unstable acrobot at upright position. Moreover, depending on the initial condition, the RL agent is able to swing up and stable the acrobot as shown in figure 3.
If you are interested in this topic, we recommend you to see [1,2].
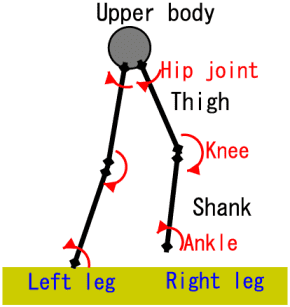
3. Biped Locomotion
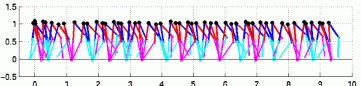
The control of biped locomotion, depicted in figure 5, is very challenging and interesting task because the biped robot has a large number of degrees of freedom similar to human lower body, and is a highly unstable dynamic system. Animal rhythmic movements such as locomotion are considered to be controlled by neural circuits called central pattern generators (CPGs), which generate oscillatory signals. We develop a new RL method using CPG controller, which is inspired by such a biological mechanisms, to automatic acquisition of bipedal locomotion. Figure 6 show the typical control process obtained by our learning method. As you can see, the sequence shows the stable biped locomotion.
If you are interested in this topic, we recommend you to see [3].

Reference
- Ishii, S., Yoshimoto, J. Yoshida, W. & Sato, M. (2000). On-line EM algorithm and its applications. in Proceedings of Emerging Knowledge Engineering and Connectionist-Based Information Systems, pp.17-20.
- Yoshimoto, J., Ishii, S. & Sato, M. (1999). Application of reinforcement learning to balancing of acrobot. in Proceedings of 1999 IEEE International Conference on Systems, Man and Cybernetics, V, pp.516-521, IEEE.
- Sato, M., Nakamura, Y., & Ishii, S. Reinforcement learning for biped locomotion. International Conference on Artificial Neural Networks (ICANN 2002), Lecture Notes in Computer Science, 2415, Springer-Verlag, pp.777-782 (2002).